Comparing Reshetikhin-Turaev skein module with the Kauffman bracket skein module of the figure-eight knot complement
Main Article Content
Article Sidebar
Abstract
The Jones polynomial is a knot invariant introduced by V. F. R. Jones in 1984 [5]. N. Rashetikhin introduced a version of the Jones polynomial using quantum groups for framed knots and links [9]. Several other polynomial invariants followed after Jones’ discovery, one closely related to the Jones polynomial known as the Kauffman bracket of framed knots and links discovered by L. Kauffman [6]. The Kauffman bracket has a simpler form than the actual Jones polynomial in the Reshetikhin-Turaev normalization.
Witten explained [10] that the Jones polynomial of a knot K comes with a sequence of colored Jones polynomials using Chern- Simons theory. This fact was proved by Reshetikhin and Turaev. The first in this sequence is the actual Jones polynomial which corresponds to the 2-dimensional irreducible representation of , and the th colored Jones polynomial of a knot , denoted by , corresponds to the coloring of by the st irreducible representation. An analogous theory was developed for the Kauffman bracket by Blanchet, Habegger, Masbaum, and Vogel in [1]. Both the Kauffman bracket and the Jones polynomial in the Reshetikhin-Turaev normalization of a knot or link in can be computed using skein relations, that give rise naturally to skein modules, first introduced by Jozef Przytycki [8], which are algebraic structures constructed from knots and links in a 3-manifold using skein relations. Let denote a framed knot (or link). The Kauffman bracket denoted by is computed by skein relations described in fig.1.
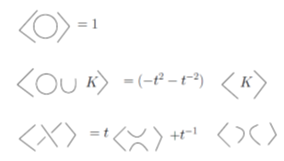
Fig. 1. Skein relations describing the Kauffman bracket
Note that here and below  is the unknot. The Jones polynomial, denoted by is determined by the following skein relations given in fig. 2, derived by R. Kirby and P. Melvin [7], and the associated skein modules were introduced by R. Gelca and A. Uribe in [4].
is the unknot. The Jones polynomial, denoted by is determined by the following skein relations given in fig. 2, derived by R. Kirby and P. Melvin [7], and the associated skein modules were introduced by R. Gelca and A. Uribe in [4].
To construct the skein module, let M be an orientable 3-dimensional manifold and let , be the set of isotopy classes of framed links in M , including the empty link. Consider the free module over with basis , denoted by . Define S(M) to be the smallest submodule of containing all the expressions of the form shown in figure 2, where the links in each expression are identical except in an embedded ball, where they look as depicted. The Reshetikhin-Turaev skein module, ,of M is defined to be the quotient .

Fig. 2. Skein relations describing the Jones polynomial
In the case of the Kauffman bracket, the Kauffman bracket skein module , is obtained by factoring by the skein relations given in fig. 1. Here we look at the specific example of the skein module of the figure- eight knot complement. The Kauffman bracket skein module of the figure-eight knot complement was computed by D. Bullock and W. Lofaro in [2]. It should be noted that much further results have been derived in the setting of Kauffman bracket skein module of the figure-eight knot complement by R. Gelca and J. Sain [3].
The main purpose of this paper is to present the relationship between Reshetikhin-Turaev skein module and the Kauffman bracket skein module of the figure-eight knot complement.
How to Cite
Article Details
Reshetikhin-Turaev skein module, Kauffman bracket skein module, figure-eight knot, Jones Polynomial
[2] Doug Bullock and Walter LoFaro (2005). The Kauffman Bracket Skein Module of a Twist Knot Exterior. Algebraic & Geometric Topology, 5(1):107-118.
[3] Razvan Gelca and Jeremy Sain (2004). The Computation of the Non-Commutative Generalization of the A-polynomial of the Figure-Eight Knot. Journal of Knot Theory and Its Ramifications, 13(06):785-808.
[4] Razvan Gelca and Alejandro Uribe. Quantum Mechanics and Non-Abelian Theta Functions for the Gauge Group su( 2). Fundamenta Mathematica, 228.
[5] Vaughan FR Jones (1997). A Polynomial Invariant for Knots via van Neumann Algebras. pages 448--458.
[6] Louis H Kauffman. State models and the jones polynomial. Topology, 26:395– 407, 1987.
[7] Robion Kirby and Paul Melvin. The 3-Manifold Invariants of Witten and Reshetikhin-Turaev for sl(2,C). Inventiones Mathematicae, 105.
[8] Jozef H Przytycki (2006). Skein Modules of 3-Manifolds. arXiv preprint math/0611797.
[9] Nicolai Reshetikhin and Vladimir G Turaev (1991). Invariants of 3-Manifolds via Link Polynomials and Quantum Ggroups. Inventiones mathematicae, 103(1):547-597.
[10] Edward Witten (1989). Quantum Field Theory and the Jones Polynomial. Commu nicantions in Mathematical Physics, 121:351-39.
